The following are notes on what I founding interesting about the Transformer alternative, RWKV (Receptance-Weighted Key Value).
If you understand how a Transformer works, the notes are meant to be a useful diff for understanding how RWKV works. Or at least, this is the diff I wish I had a week ago; YMMV.
I'm not giving the basic sales-pitch for RWKV, about how it can be an RNN at inference-time but train in parallel; the RWKV wiki is a good source for that.
1: RWKV has the same global structure as a Transformer, without position encoding
That is, RWKV has a basic structure like:
[tokens] ->
token-encodings ->
layer norm ->
N blocks ->
||
\/
residual connection start >------|
|| |
\/ |
layer norm -> |
RWKV-time-mixing -> |
|| |
\/ |
residual connection end <--------|
||
\/
residual connection start >------|
|| |
\/ |
layer norm -> |
channel-mixing / FFN -> |
|| |
\/ |
residual connection end <--------|
||
\/
layer norm ->
output projection ->
[logits]
RWKV-time-mixing obviously replaces self-attention. The channel-mixing is more like a slight modification to the feed forward network than a replacement, but that's in the same place as well.
Note that there's no position encoder like Xpos, AliBi, and so on. This is because RWKV is naturally order-sensitive, unlike self-attention.
This whole thing should be pretty familiar.
2: RWKV blocks have varying and layer-position-specific parameter distributions
That is, the first RWKV block will be initialized with a different weight distribution than the last RWKV block.
This contrasts with Transformers, where the first and last Transformer blocks are often basically homogenous and only grow to have different weight distributions after training.
Specifically, the RWKV blocks earlier in the stack are biased to forget things quicker. Information from far back decays faster. So earlier blocks are more likely to attend to near-to-the-current-token details of the sequence, while the later blocks are more biased to attend to far-from-the-token details. The paper says this improves performance.
I know that Qwen also does something similar to this -- with sliding windows of different lengths for different layers, and shorter windows for earlier layers -- but I'm not aware of any other Transformers that use this bias.
This seems like an interesting direction, both for performance and interpretability, that could move the features of transformers to be more like those of convolutional neural networks (CNNs).
In CNNs:
- The later layers must lose details about small-scale per-pixel spatial details because max-pooling deletes spatial information; thus higher levels cannot represent things like edge detection.
- The earlier layers have smaller receptive fields, and thus these convolutions must represent the more simple features that fit into these fields (like edge detectors) rather than more complex features (like faces).
So CNNs must have the least abstract features (like edge detectors) at the lower layers, and most abstract abstract features (like face or dog detectors) at the higher layers.
Adding windows or shortened memory to earlier Transformer / RWKV layers is like limiting the receptive field of earlier CNN layers -- it's like adding the second constraint. above. But in RWKV, there's still no mechanism corresponding to how CNNs have reduced resolution at higher levels, corresponding to constraint 1.
So reducing the resolution of the Transformer layers would require more work, something like the Hourglasss transformer. Both of these seem pretty intuitively promising, although of course my intuition is crap in DL world.
3: Each RWKV block has a time-mixing block (which corresponds to attention) and a channel-mixing block (that corresponds to the feed forward network)
Each of these is composed of a layer-norm followed by some specific details.
4: Both the time-mixing block AND the channel-mixing block actually mix data over time
So the channel-mixing block is just horribly named.
Specifically, both time-mixing block and channel-mixing block do linear interpolation (with per-channel weights) between the token at time t and the token at time t-1. This happens after the layer norm but before doing anything else.
This mixture takes place according to a per-channel-index weighting, and so looks something like -- in the below x and xx have b, t, c dimensions while the time_mix variables have c dimensions.
# xx = data shifted forward one timestep
# b, t, c = x.size()
xx = self.time_shift(x)
# Mix all of the current values with prior values
# according to a PER DIMENSION mixture
# (c,) = self.time_mix_k.size()
xk = x * self.time_mix_k + xx * (1 - self.time_mix_k)
Again, something like this happens in both the time-mixing and the channel-mixing blocks.
This means that even without the WKV self-attention replacement, each token has a receptive field reaching 2 * number_of_layers into the past.
5: The channel-mixing block is a normal FFN, except (a) with a squared ReLU instead of a ReLU for the activation and an (b) extra 'forget' gate at the end.
A normal feed forward network is like O(max(0, Wx)), where W has dimensions of [channels * 4, channels], and O has [channels, channels * 4]. The channel-mixing block has O(max(0, Wx)^2) instead, and then multiplies the results of this with a sigmoid forget gate.
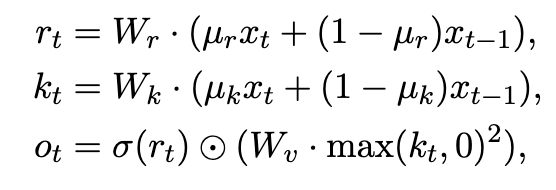
So, in the above the first two lines are mixing each token with the prior token. Then the later has the feed forward network, whose results are per-element multiplied by the results of the forget gate.
The paper doesn't really tell you what's up with the forget gate, or why it works better with it. I'm curious if this is something that helps with RWKV only, or if it would also help with a transformer, or what.
6: The time-mixing block doesn't have heads.
Small point, but a fair number of transformer variants keep the heads of multi-head self-attention -- or something like heads. RWKV drops those entirely, and has nothing like multi-head self-attention in favor of treating each channel-index differently.
7: The time-mixing has "key" values that are not keys; they are never multiplied by query values, but simply weight how important the "value" is later
The time-mixing value for each token is composed of a decaying exponential mixture of the values for past tokens, where each tokens value is is weighted by the per-token key, plus the value of the present token.
Note that the key value is a weighting for the linear mixture of past value tokens, but it is never multiplied by any "query" value like in a Transformer's self-attention. So it's an absolute measure of importance, rather than a measure of importance relative to some query.
Not multiplying the query and key values, of course, is why we don't have the quadratic complexity that self-attention does.
Note that the decaying exponential mixture is again per-channel index.
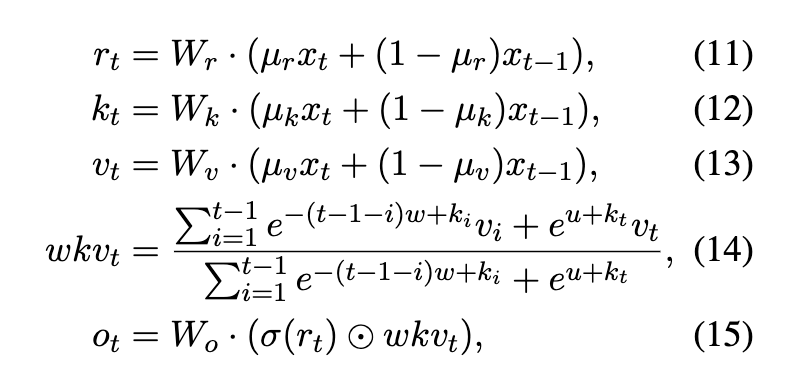
These weights are initialized differently per-layer, as mentioned above.
Fin
I have no ending, these are just my pretty minimal notes really. :)