Experiments With Algorithm Distillation, Part 1

I was excited about the Algorithm Distillation paper from DeepMind when it came out about a month ago.

This is the start of my efforts to reproduce it, although for now I've only worked with the simple case of the n-armed-bandit.

Background

Algorithm distillation can be viewed as an extension of the Decision Transformer.

The decision transformer (and the large body of work following up on it) extend the generalizing power of the transformer to reinforcement learning. The decision transformer learns a policy for a specific environment and specific task, from a dataset where each dataset entry is a sequence of states, actions, and returns-to-go from an agent acting in that environment. The policy acquired by the decision transformer learning to predict the action of this agent, can then be deployed in the same environment on the same task.

An important limit on the decision transformer is that it cannot learn from scratch. It depends on saved training data from another reinforcement learning algorithm -- or from a human learning who has manually produced imitation data. It is only good in the offline setting; it is useless in the online setting, where it has to act itself without anyone to imitate.

So the process of learning itself is not incorporated into a decision transformer, although the expertise of some agent is.

The algorithm distillation paper begins to indicate how a transformer can begin to learn the process of learning.

It's a very simple idea. Rather than learn simply from in-episode sequences, an algorithm distillation transformer learns from cross-episode sequences. In theory this should allow it to model the process of learning itself, because the improvement of the agent is evident from cross-episode sequences.

In practice it still somewhat limited. As described by this post, the paper only shows that the decision transformer can "learn to do better" on extremely similar tasks. I remain interested in this nevertheless.

Reproduction of N-Armed Bandit

The agent from which my transformer learned was an optimistic n-armed-bandit. This is a standard algorithm which starts out with very high estimates for the value of each arm in the bandit. So it starts off by trying each arm, because each time it tries something it gets much less than it "expects" and so selects something else next time, until it converges on the arm with the highest average result.

I start the algorithm off with an estimate of 15 as the mean value returned by each arm, while in actuality each arm has a mean value centered around zero with a standard deviation of one. Even the best of the ten arms is unlikely to have a value higher than 3.

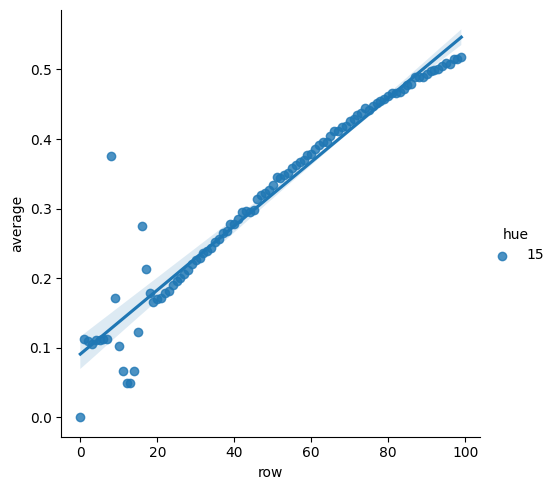
correct for pessimistic agent

The above shows the percent of the time the agent picks the arm with the highest reward over the course of a hundred steps, over 32,000 runs.

(Note the spike early on in the training. That's because after pulling each arm once for the initial exploration, the next arm that it pulls tends to be the correct arm, because that's the one that was most likely to give the highest return.)

The first interesting thing about an algorithm distillation transformer imitating this is that even when the transformer is quite inaccurate, you can still do quite well in terms of the percent correct that it gets.

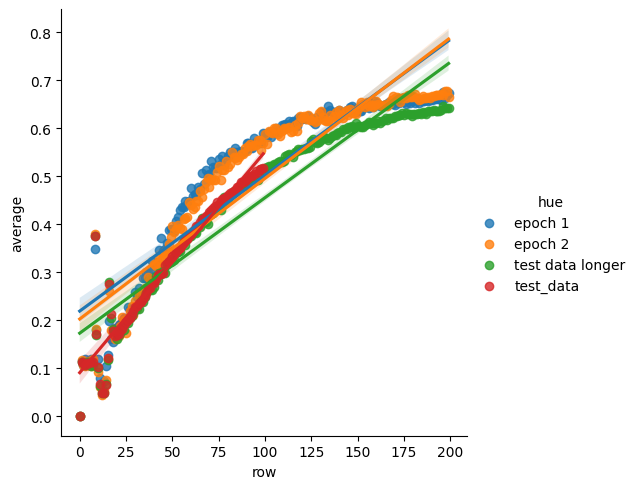
correct for AD transformers

Note that the orange and blue actually do better in terms of how frequently they select the correct arm them the data they are trained from! After further training they actually get worse as they adhere more closely to the training data.

I'm not sure why this is. I am sure that this happens; I checked my data several times.

Note also that the algorithm distillation transformer still learns up to two hundred steps, even though it was only trained on a hundred steps of data! So it generalizes out of distribution at least a tiny bit.

The other fun thing is what happens when the algorithm distillation transformer acts in an environment where the first arm always has the highest value, even though the transformer learned to act in a situation where the highest arm was never the first.

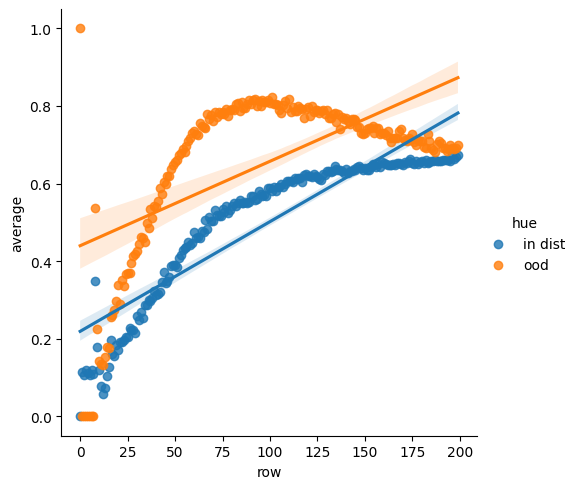
correct for AD transformers

Once again it learns to act correctly! But note that here it fails to generalize much past a hundred steps -- it actually starts to get worse as it gets more data.