Softplus Gated Attention > Sigmoid Gated Attention

Gated Attention Improved by Using Softplus

TLDR

Using softplus rather than sigmoid as an activation function for the gate in a gated attention Transformer notably improves performance, just as gated attention itself seems to improve performance over vanilla attention.

In my small testbed, softplus is ~10% to ~30% faster than sigmoid at reaching equal loss, or ~25% to ~50% faster than non-gated attention, with the effect possibly (?) increasing with size.

The effect seems robust across every size I've tested, although as a GPU-poor person I've only gone up to 2 billion tokens and 95 million parameters.

Architecture

The Qwen team recently published a study of gated attention.

In the mainline dense implementation (at "G1" in the paper, with a sigmoid), this introduces a multiplicative per-channel rescaling of the concatenated outputs of MHA, where each channel is scaled according to a gate learned from the per-token input to the attention.

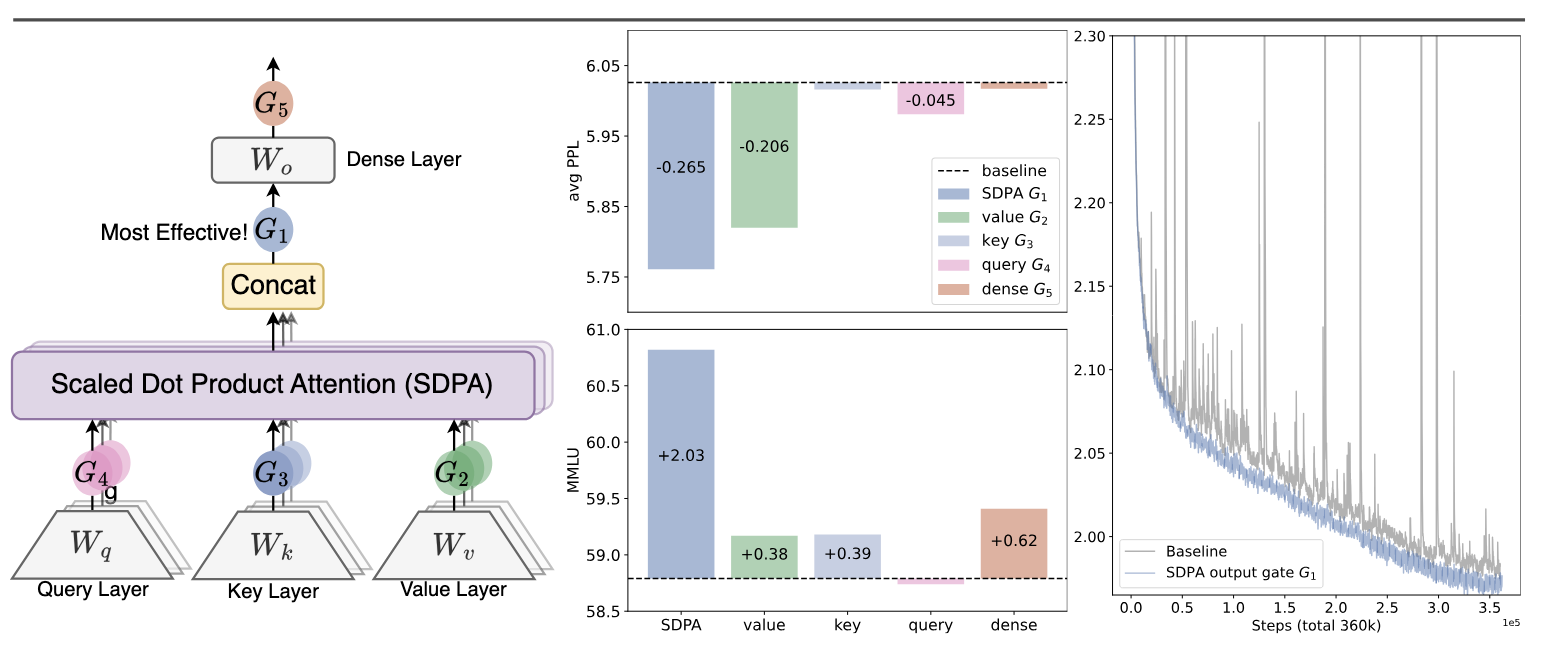
This requires a new dim_model x (num_head x dim_head) parameter linear layer -- in practice just dim_model^2 -- that per-token and per-channel modulates the output of MHA.

This is simple to implement -- here's it added to nanoGPT:

class CausalSelfAttention(nn.Module):

    def __init__(self, config):
        super().__init__()
        assert config.n_embd % config.n_head == 0

        self.c_attn = nn.Linear(config.n_embd, 3 * config.n_embd, bias=config.bias)
        self.c_proj = nn.Linear(config.n_embd, config.n_embd, bias=config.bias)
        # New!
        self.gate = nn.Linear(config.n_embd, config.n_embd, bias=False)
        # etc etc etc

    def forward(self, original_input):
        # ... get results for attention @ qkv
        # blah blah blah
        # y here is the output of multi-head attention

        # Shape it
        y = y.transpose(1, 2).contiguous().view(B, T, C)
        # Elementwise multiplication with activation_func(gate_output)
        y = y * your_activation_function(self.gate(original_input))
        return self.c_proj(y)

When the activation function above is sigmoid, the paper reports notably improved performance. This matches at least one other paper that has found improved stability / quantilizablity through such sigmoid gating. They don't try many other activation functions.

I follow the Qwen team in reducing the expansion of the FFN from 4.0 to 3.5 to keep parameter count equal.

The following improves performance further:

• Replace the sigmoid function with softplus
• Zero out the weights for the initial linear gate, so the input to softplus will be 0, and the gate will have value of ~0.693, to start.

(In practice, only the first is probably necessary. But in small scales this reduces variance, and starting out with a no-op pass-through gate feels more elegant to me, so that's what I've stuck with.)

Here is the per-step performance across multiple (albeit tiny) scales. At each scale, softplus is the best, followed by sigmoid, followed by the base model. (This is per-step chart, but time is about equal for each equally-sized networks, and the softplus-based model is always best.)

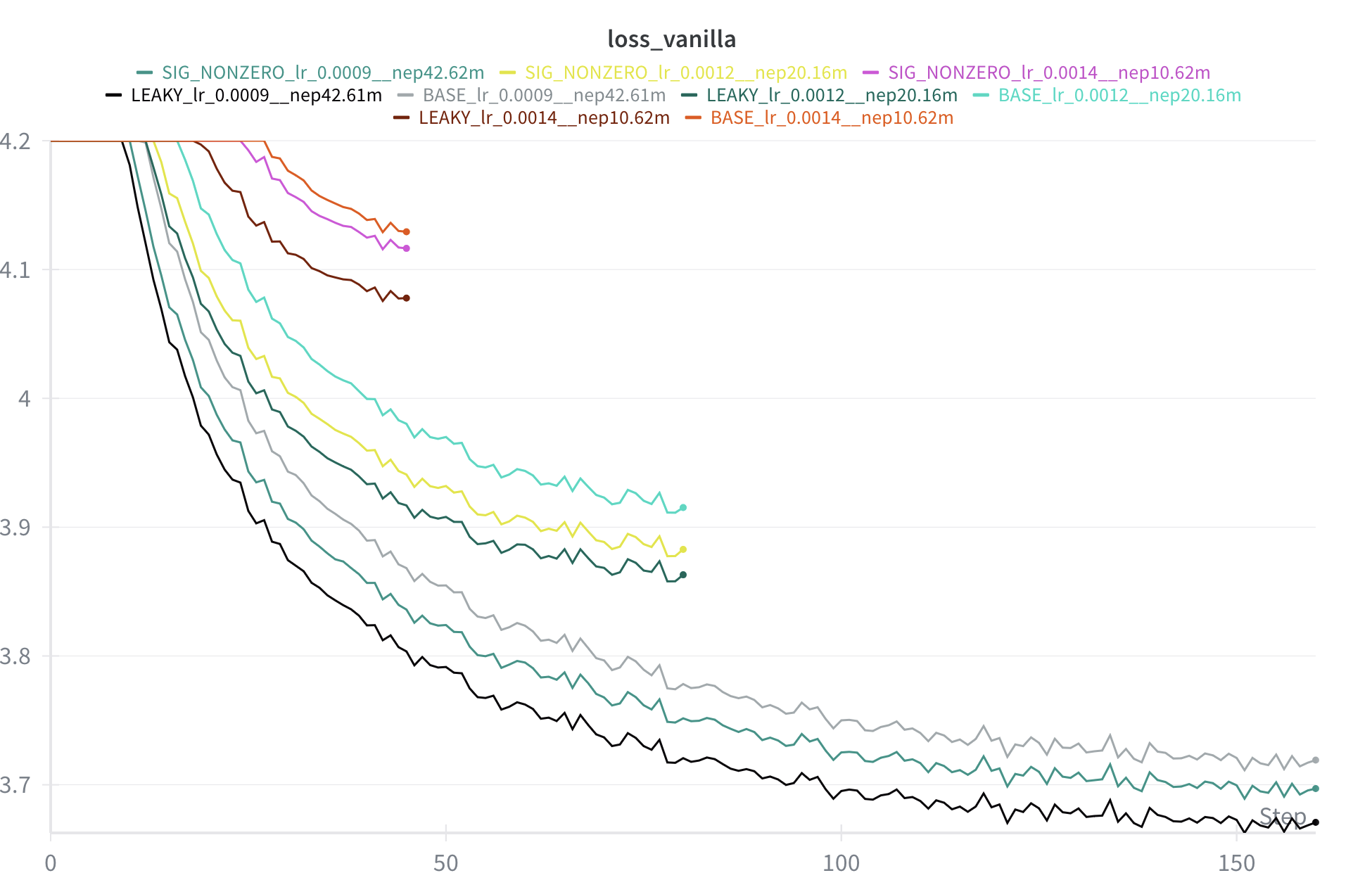
Gains are pretty robust. My hyperparameters are probably not ideal, but these results are typical across a range of scales, learning rate schedules, and architecture modifications that I've tried.

Further Notes:

1. Percentage improvement in time-to-equal loss seems to get larger as we scale up, (~30% -> ~50%). I'm not extremely confident about this; it might be due to a less-than-ideal hyperparameters. But given the link between gated attention and outliers at large scales in prior work, I find it plausible that performance gains could continue to increase with scale indefinitely.

2. While the improvement of sigmoid-gating over normal attention in very shallow Transformers (4-6 layers) is small, softplus gating seems to handle this somewhat degenerate case rather better.

3. Softplus obviously has a number of factors that make it more attractive than sigmoid. Sigmoid gating limits channel scaling to (0,1), and so allows the self-attention layer to output nothing easily. Softplus, however, allows both attenuation (~0) and amplification (>1) with non-vanishing gradients.

I've explored the space of similar functions for a bit (exponential, softer / harder softplus) and haven't found any similar function that improves upon it.

4. I think it would be worthwhile scaling this past the ~10 hours on a 4090 scale.

Trying Elsewhere

I did all these changes on my own LLM testbed, but to confirm that it worked I checked against the character-based training in NanoGPT.

Notes on making this work:

1. Increased size of training text by about 120x, so we're not massively overtraining, and adding shuffling.
2. Dropping positional encoding for rotary encoding.
3. (Selecting zero dropout, and zero biases, of course).

Subsequently we again find that once again softplus > sigmoid > base performance at 7000 steps across multiple seeds, although by relatively small amounts given the very small scale.

Character-based NanoGPT differs from my setup in weight initialization methods, in lacking QK norm, in using GELU rather than ReLU squared for the MLP activation function, in using LayerNorm rather than RMS norm, and probably other stuff that I've missed. So the improvements from this change seem reasonably robust.

Appendix

All results on a 4090 with FineWeb, one run each.

Also all the math is from me eyeballing charts on WanDB; I tried to look carefully but take it for what it is

## 10.62m params @ 300 million tokens, 18 minutes:

Final loss:
base - 4.13
sigmoid - 4.12
softplus - 4.08

softplus reaches ~4.13 @ ~12 minutes
(18 - 12) / 18 ~ 33% speedup
softplus reaches ~ 4.12 @ ~13 minutes
(18 - 13) / 18 ~ 27% speedup

---

## 20.16m params @ 530 million tokens, 49 minutes:

base - 3.91
sigmoid - 3.88
softplus - 3.86

softplus reaches 3.91 @ ~29 minutes
(49 - 29) / 49 ~ 40% speedup
softplus reaches 3.88 @ ~42 minutes
(49 - 42) / 49 ~ @ 14% speedup

---

## 42.62m params @ 1 billion tokens, 165 minutes:

base - 3.72
sigmoid - 3.69
softplus - 3.67

softplus reaches 3.72 @ ~82 minutes
(165 - 82) / 165 ~ 50% speedup

softplus reaches 3.69 @ ~115 minutes
(165 - 115) / 165 ~ 30% speedup

---

## 73.73m params @ 1.6 billion tokens, 350 minutes:

base - 3.58
softplus - 3.52

softplus reaches 3.58 @ ~166 minutes
(350 - 166) / 350 ~ 51% speedup

---

## 95m params @ 2.1 billion tokens, 540 minutes:

base - 3.514
sigmoid - 3.486
softplus - 3.451

softplus reaches 3.514 @ ~255 minutes
(540 - 255) / 540 ~ 52% speedup

softplus reaches 3.486 @ 337
(540 - 337) / 540 ~ 36% speedup