MoE and Dense Transformers Maybe Learn the Same Thing

Here's a continuation of the same question as before: Given that they are trained to the same overal loss, do MoE transformers learn different things from dense Transformers?

My gut still says that they should learn different things. New, more detailed results still seem to point against my gut somewhat.

Here's what I did:

• Trained a 211m MoE transformer and a 135m dense transformer to about identical loss on 1.2b tokens, once again using exactly the same tokens in the same order. Last time I did only ~500m tokens. I also used a tokenizer with a bigger vocabulary, so this is closer to ~6 times as much data than to ~2 times as much.
• For MoE, once again routed to a single expert switch-transformer style, with just 8 experts per MoE layer. 4 MoE layers out of a total of 9 layers.
• New: Saved the per-token loss on a test set every 2,000 steps, so now I have ~50 time-slices per token loss as the training progresses.

(There are further hyperparameter details below + a notebook. Try the notebook at your own peril.)

I can now find the r^2 correlation between the per-token losses for different models all through the training. Before, I only could look at the per-token loss correlation at the end of the training.

Notably, it looks like the r^2 between the MoE and the dense transformer increases as time goes on.

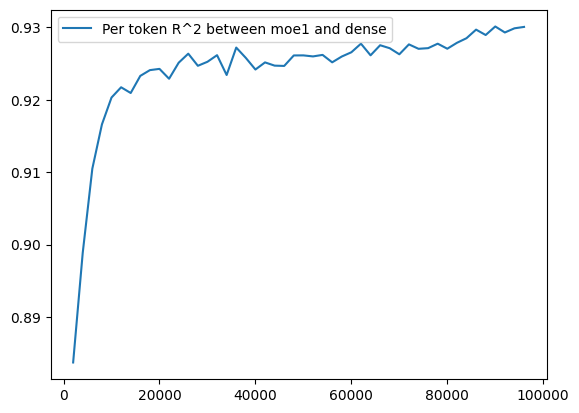
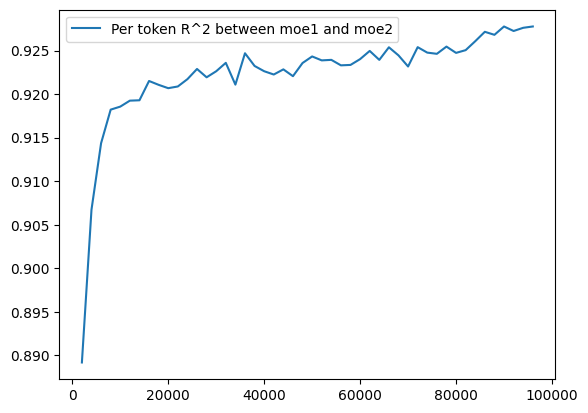
Unfortunately, if we've trained two identical-except-for-seed MoEs, we find that their progressive per-token correlation looks exactly the same -- except a little less similar.

Once again, we find that there is greater similarity between MoE and dense than between MoE and MoE.

By contrast, the per token correlation -- even between two slightly differently sized dense models -- starts off very similar and remains very similar.

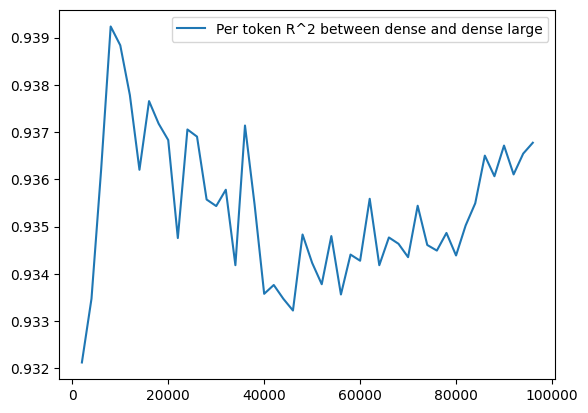
(Note: I'm pretty intrigued by the U-shape here? It might be random chance, though, especially because this is all happening in a very small range.)

My conclusion? Well:

1. MoEs -- at least as I build them -- probably just start off with a stronger, totally random prior. This means they are less guided by the data.

2. The MoEs then become less dissimilar from each other and from the dense transformer, because (of course?) they're just fitting the same data.

3. At this level of abstraction, MoEs do not systematically learn something different from Dense transformers, otherwise we would not have consistently higher correlation between Dense-MoE than we do between MoE-MoE.

I think that there's at least some chance that in the limit of maybe 10x or 100x more tokens than I've trained on, we'd find this curve of greater similarity become an upsidedown U-shape, if the maxed-out capacity of the MoE and the dense transformer leads to different fitting of the data. These networks are still massively undertrained, so it could happen.

But. That also might not happen, and I'm increasingly uncertain that it would happen, or happen in any kind of a way that matters.

I think that's the only place left for this some difference to reveal itself, at least for this particular architecture.

(This could, maybe be a big difference -- probably even a small difference in coverage, at a very low loss, amounts to substantially different knowledge. I was originally interested in this question because of Llama3 not being dense; I remain puzzled by this.)

One important question would also be the scaling of this difference. As MoEs get larger, does this between MoE difference increase, so that different random sees matter more, or does it decrease, so it matters less?

Hyperparameters

• 9 layers each
• 1100 hidden dim dense, 792 MoE
• 4 MoE layers in MoE, 8 experts per layer
• 840 ctx len
• Hard-Alibi attention
• layernorm(attention(layernorm(x)))
• ff(layernorm(x))
• FF expansion of 4
• grad clip 0.9
• vocab 2048
• maybe 5,000 Gutenberg books as data, 1 epoch
• 1.2b tokens
• batch size 16
• lr 0.0001, warmup 2000 steps
• lr reduced linearly to 1/10
• aux balancing loss for MoE scaled by 0.0625

Notebook